Baccalauréat STI2D et STL/SPCL - Polynésie 21 juin 2018 - Exercice 4

Page 7 sur 8: Exercice 4

Exercice 4 6 points

Fonctions et calcul intégral

 

Partie A

On donne ci-dessous la courbe représentative d'une fonction $f$ définie sur $\mathbb R$. La droite $(d)$ est tangente à cette courbe au point d'abscisse 0.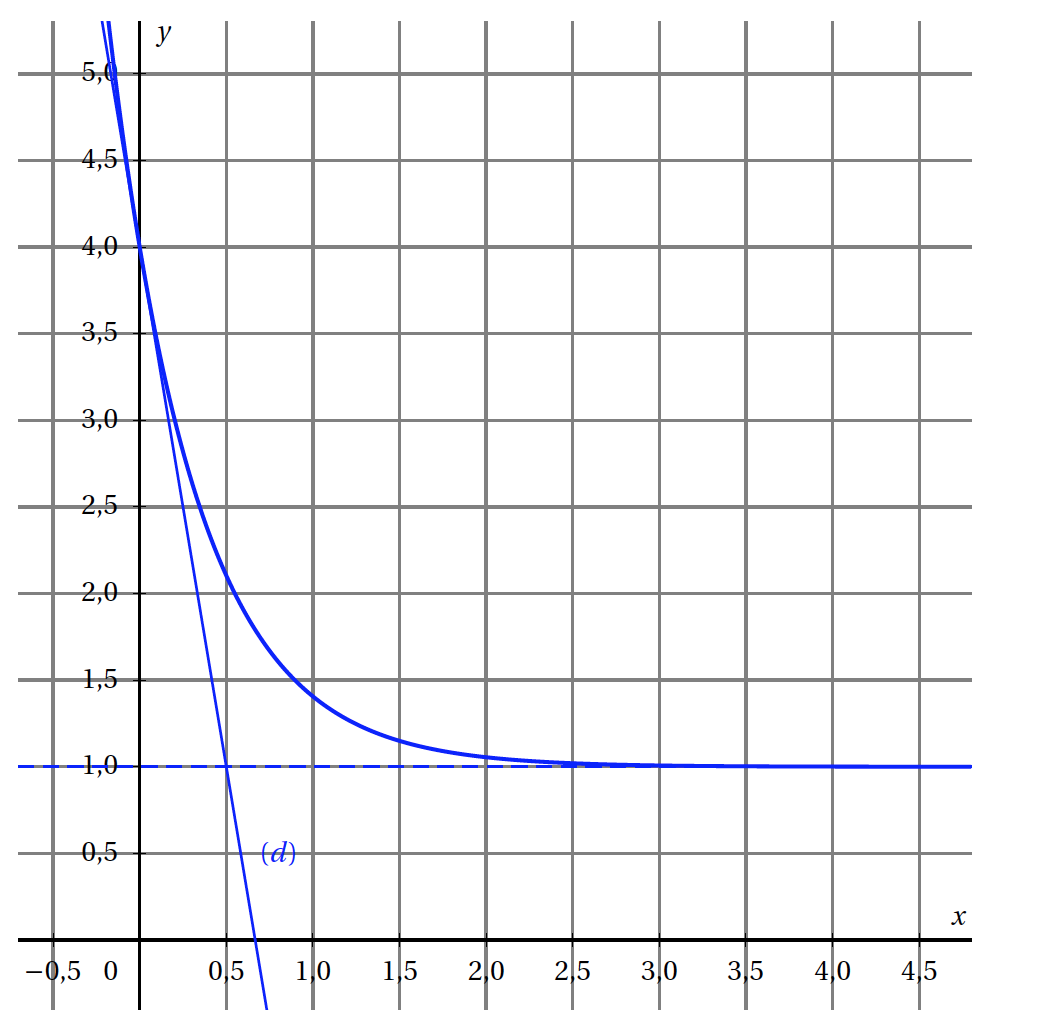

Donner par lecture graphique:

1. La valeur de $f(0)$.
2. La limite de $f$ en $+\infty$.
3. Le tableau de variation de $f$.
4. Le coefficient directeur de la tangente $(d)$ à la courbe représentative de $f$ au point d'abscisse 0.

Partie B

On considère l'équation différentielle $y'+2y=2$ dans laquelle $y$ est une fonction de la variable réelle $x$ définie et dérivable sur $\mathbb R$. On admet que la fonction représentée dans la Partie A est la solution de cette équation différentielle vérifiant $f(0)=4$.

1. Démontrer que, pour tout réel $x$, on a $f(x)=3\text{e}^{-2x}+1$.
2. Retrouver, en justifiant par des calculs, les résultats obtenus aux questions 2. 3. et 4. de la partie A.

Partie C

L'unité graphique est le dm (décimètre). On a représenté graphiquement ci-dessous la fonction $f$ sur l'intervalle $[0~;~4]$. On appelle $\mathcal{C}$ la courbe obtenue.

On fait tourner la courbe $\mathcal{C}$ autour de l'axe des abscisses. On génère ainsi une surface dans l'espace ayant la forme d'un vase représenté ci-après en coupe et en perspective.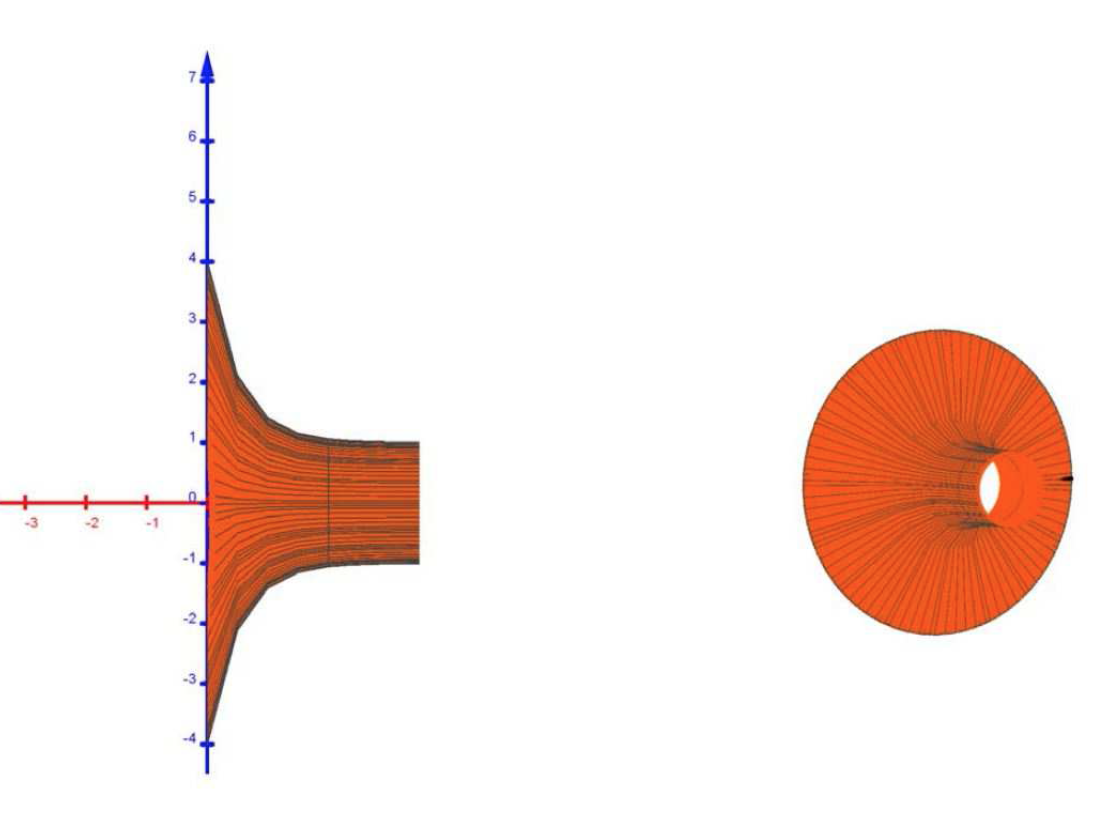

Le volume de ce vase, en dm$^3$, est donné par: $$V=\pi \times\displaystyle \int_{0}^{4} \left (f(x)\right )^2 \text{d} x.$$

1. Montrer que, pour tout $x \in [0~;~4]$, on a $\left ( f(x)\right )^2 = 9\text{e}^{-4x} + 6\text{e}^{-2x}+1$.
2. Calculer le volume du vase, exprimé en dm$^3$. On donnera la valeur exacte puis une valeur approchée à $10^{-2}$ près.
3. On désire remplir ce vase aux deux tiers du volume avec du sable coloré qui est vendu par sac de 3 dm$^3$. Déterminer le nombre minimum de sacs qu'il faut acheter.