Baccalauréat STI2D et STL/SPCL - Polynésie 21 juin 2018 - Correction Exercice 2

Page 4 sur 8: Correction Exercice 2

Correction de l'exercice 2 (5 points)

Suites et Probabilités

Les deux parties de l'exercice sont indépendantes.

Partie A

Dans cette partie on s'intéresse à l'évolution, depuis 2010, du nombre de véhicules « 100% électriques » en France. Le 24 mars 2017, l'association nationale pour le développement de la mobilité électrique (Avere-France) a publié l'article suivant:

La France célèbre son 100ieme véhicule

« 100% électrique », une première en Europe

Jeudi 23 mars, le marché français des véhicules particuliers et utilitaires « 100% électrique » a franchi le cap des $100\;000$ immatriculations cumulées depuis 2010, date de lancement de la nouvelle génération de véhicules électriques. La France devient alors le premier pays européen à atteindre un tel parc de véhicules avec zéro émission.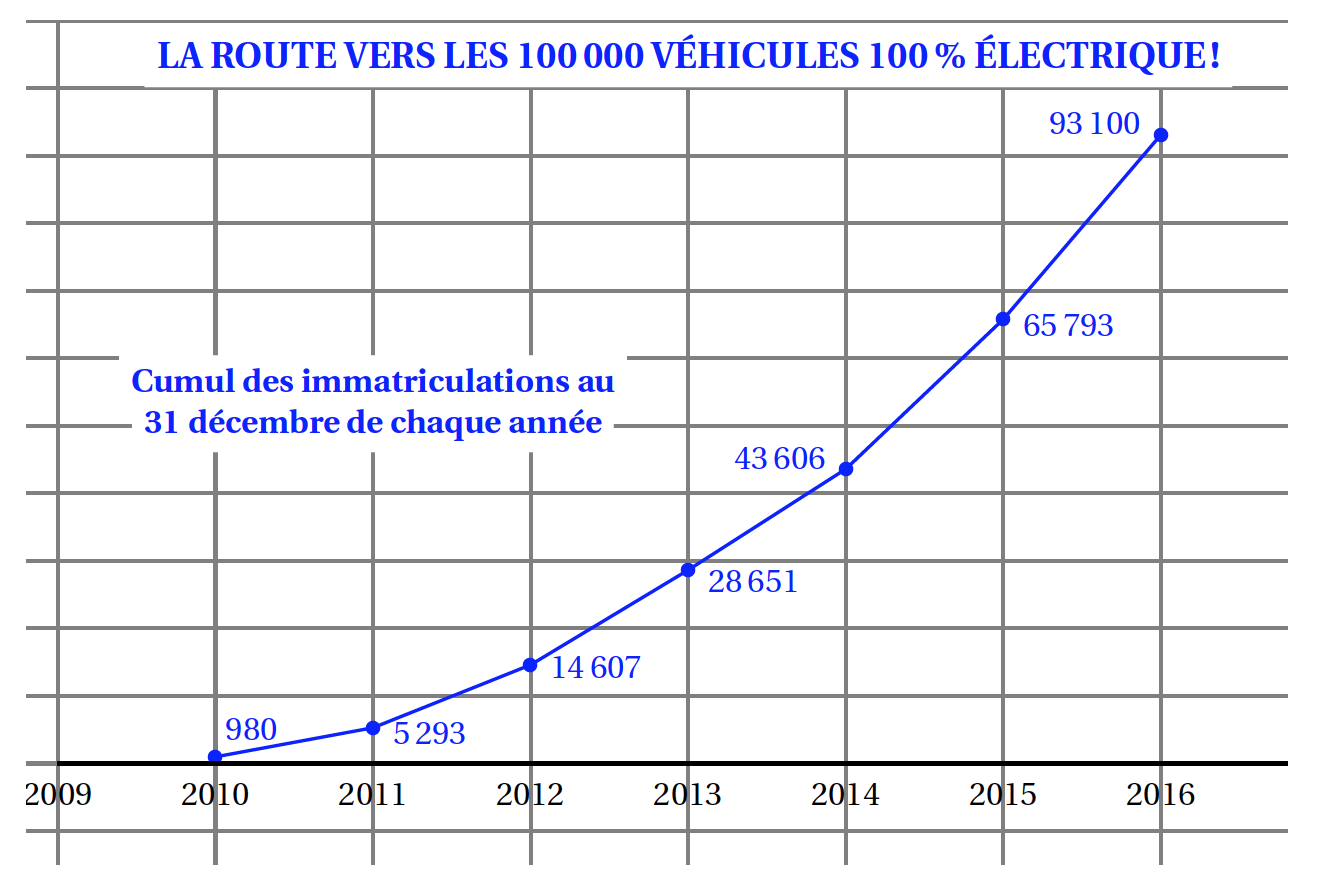

Dans ce contexte économique et environnemental, l'Avere-France estime qu'à l'horizon 2020, la France devrait compter plus de $350\;000$ véhicules « 100% électrique » immatriculés.
D'après l'association Avere-France
La lecture du graphique précédent permet, par exemple, de dire qu'au 31 décembre 2015, il y avait en tout $65\;793$ véhicules « 100% électrique » immatriculés.

1. Déterminer le pourcentage d'augmentation, entre le 31 décembre 2015 et le 31 décembre 2016, du nombre de véhicules « 100% électrique » immatriculés en France. Arrondir le résultat à 1%.
$$\left (\dfrac{93100}{65793}-1\right )\times 100\approx 41,5$$ Entre le 31 décembre 2015 et le 31 décembre 2016, le nombre de véhicules « 100 % électrique » immatriculés en France a augmenté d'environ 42 %.

On suppose qu'à partir de l'année 2017, l'augmentation annuelle de véhicules « 100% électrique » immatriculés en France sera constante et égale à 40%. Dans le cadre de ce modèle, pour tout entier naturel $n$, on note $u_n$ une estimation du nombre de véhicules « 100% électrique » immatriculés en France au 31 décembre de l'année $2016+n$. Ainsi on a $u_0 = 93\;100$.

2. 1. Déterminer le nombre de véhicules « 100% électrique » en France au 31 décembre 2017.
   $$u_1=93100\times \left(1+\dfrac{40}{100}\right)=93100\times 1,4=130340$$
   2. Déterminer la nature de la suite $(u_n)$.
   Le coefficient multiplicateur associé à une augmentation de 40 % est égal à 1,4.
   Pour tout entier naturel $n$, on a $u_{n+1}=1,4⁢u_n$. Par conséquent, $\left(u_n \right)$ est une suite géométrique de raison $q=1,4$.
   3. L'affirmation de l'association Avere-France figurant à la fin de l'article est-elle validée par le modèle proposé? Justifier la réponse.
   $\left(u_n \right)$ est une suite géométrique de raison $q=1,4$ et de premier terme $u_0=93100$ donc pour tout entier naturel $n, u_n=93100\times 1,4^n$.
   On en déduit que : $$u_4=93100\times 1,4^4\approx 357653$$ Selon ce modèle, il devrait y avoir plus de 357 600 véhicules « 100 % électrique » immatriculés en France au 31 décembre de l'année 2020. Ce résultat est conforme avec l'estimation de l'association Avere-France.
3. À l'aide d'un algorithme, on souhaite estimer l'année au cours de laquelle le nombre de véhicules « 100% électrique » immatriculés en France dépassera  $1000\;000$ avec ce modèle.
   1. Recopier et compléter l'algorithme suivant afin qu'il réponde au problème.
      $$\begin{array}{|l|} \hline n \leftarrow 0 \\ u \leftarrow 93\;100 \\ \text{Tant que } \cdots\\ \hspace{1cm} n \leftarrow \cdots \\ \hspace{1cm} u \leftarrow \cdots\\ \text{Fin Tant que}\\ \hline \end{array}$$
   $$\begin{array}{|l|} \hline n \leftarrow 0 \\ u \leftarrow 93\;100 \\ \text{Tant que }u < 1000000\\ \hspace{1cm} n \leftarrow n+1 \\ \hspace{1cm} u \leftarrow 1,4\times u\\ \text{Fin Tant que}\\ \hline \end{array}$$
   2. Laquelle des variables $n$ ou $u$ est-il utile d'afficher après l'exécution de cet algorithme pour répondre au problème?
   Il convient d'afficher la variable $n$ qui contient le nombre d'années depuis 2016 pour que le nombre de véhicules « 100 % électrique » immatriculés en France dépasse 1 000 000.
   3. Quelle est la valeur de cette variable?
   pour tout entier naturel $n, u_n=93100\times 1,4^n$ $$\begin{array}{rll} u_n <1 000 000 & \iff 93100\times 1,4^n <1 000 000. &\\ & \iff 1,4^n <\frac{1 000 000}{93100}&\\ &\iff 1,4^n < \frac{10 000}{931}&\\ &\iff \ln\left (1,4^n\right ) <\ln \left (\frac{10 000}{931}\right )& \ln \text{est strictement croissante sur } ]0;+\infty[\\ &\iff n\ln\left (1,4 \right ) <\ln \left ( \frac{10 000}{931}\right )& \text{ car } \ln\left (a^n \right )=n\ln a\\ &\iff n< \dfrac{\ln \left (\frac{10 000}{931}\right )}{\ln\left (1,4 \right )}&\text{ car } 1,4 >1 \text{ donc } \ln\left (1,4 \right ) >0\\ \end{array}$$ Grâce à une calculatrice, on obtient $\dfrac{\ln \left (\frac{10 000}{931}\right )}{\ln\left (1,4 \right )} \approx 7,06$.
   donc le plus petit entier $n$ solution de l'inéquation $u_n>1000000$ est $n=8$.
   La valeur de la variable $n$ obtenue à la fin de l'execution de l'algorithme est $n=8$.
   4. Interpréter cette valeur dans le contexte de l'exercice.
   Selon ce modèle, c'est en 2024 que le nombre de véhicules « 100 % électrique » immatriculés en France dépassera 1 000 000.

Partie B

Une usine fabrique des batteries Lithium-Ion, garanties 4 ans, nécessaires au fonctionnement des véhicules « 100% électrique ». La durée de vie moyenne d'une telle batterie s'élève à 7 ans. On admet que la variable aléatoire $T$ qui, à une batterie Lithium-Ion prélevée au hasard dans le stock de l'usine, associe sa durée de vie, exprimée en années, suit la loi exponentielle de paramètre $\lambda$.

1. Déterminer la valeur exacte de $\lambda$.
L'espérance mathématique de la variable $T$est $E(T)=\dfrac{1}{\lambda}$ d'où : $$\dfrac{1}{\lambda}=7 \iff \lambda \dfrac{1}{7}$$ $T$suit une loi exponentielle de paramètre $\lambda \dfrac{1}{7}$.
2. Pour la suite, on prendra $\lambda = 0,143$.
   1. Déterminer la probabilité qu'une batterie Lithium-Ion soit encore en état de fonctionnement au bout de 8 ans. On donnera une valeur approchée à $10^{-3}$ près.
   La densité de la variable aléatoire $T$ suivant une loi exponentielle de paramètre $\lambda =0,143$ est la fonction $f$ définie pour tout réel $t$ de l'intervalle $[0;+\infty[$ par $f(t)=0,143 =0,143⁢e^{-0,143⁢t}$ d'où : $$\begin{array}{cl} P(T\geq 8) & 1-P(T<8)\\ &= 1- \displaystyle \int_0^8 0,143⁢e^{-0,143t}\; dt \\ & =1-\left [ -e^{-0,143t} \right ]_0^8\\ &=1- \left (-e^{-0,143\times 8} -(-1)\right ) \\ &= e^{-1,144}\\ &\approx 0,319 \end{array}$$ La probabilité qu'une batterie Lithium-Ion soit encore en état de fonctionnement au bout de 8 ans est $P(T\geq 8) \approx 0,319$.
   2. Déterminer la probabilité qu'une batterie Lithium-Ion tombe en panne avant la fin de la garantie. On donnera une valeur approchée à $10^{-3}$ près.
   $$\begin{array}{cl} P(T\leq 4) & = \displaystyle \int_0^4 0,143⁢e^{-0,143t}\; dt \\ & = \left [ -e^{-0,143t} \right ]_0^4\\ &= \left (-e^{-0,143\times 4} -(-1)\right ) \\ &= 1- e^{-0,572}\\ &\approx 0,436 \end{array}$$ La probabilité qu'une batterie Lithium-Ion tombe en panne avant la fin de la garantie est $P(T\leq 4 ) \approx 0,436$.
   3. Déterminer le réel $t_0$ tel que $P(T>t_0)=0,75$. On donnera la valeur exacte et la valeur arrondie à l'unité. Interpréter le résultat dans le contexte de l'exercice.
   $$\begin{array}{cl} P(T\geq t_0) =0,75&\iff 1-P(T < t_0)=0,75\\ &\iff P(T< t_0)=0,25\\ &\iff \displaystyle \int_0^ {t_0} 0,143e^{-0,143t}\; dt =0,25 \\ &\iff \left [ -e^{-0,143t} \right ]_0^{t_0}=0,25\\ &\iff \left (-e^{-0,143\times t_0} -(-1)\right ) =0,25 \\ &\iff 1- e^{-0,143\times t_0} =0,25 \\ &\iff e^{-0,143\times t_0} =0,75 \\ &\iff -0,143t_0=\ln(0,75) \\ &\iff t_0= \dfrac{\ln(0,75)}{-0,143}\\ &\textbf{ soit} t_0\approx 2 \end{array}$$ La probabilité qu'une batterie Lithium-Ion fonctionne plus de deux ans est égale à 0,75.