Baccalauréat STI2D et STL spécialité SPCL Antilles-Guyane 16 juin 2017 - Correction Exercice 3

Page 6 sur 8: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Fonctions ln

Dans cet exercice, $\ln$ désigne la fonction logarithme népérien et l’unité de longueur est le mètre (m). Un ingénieur prépare un plan pour fabriquer la voile d'un petit bateau. La voile est représentée en gris dans le repère orthonormé ci-dessous où une unité représente un mètre.

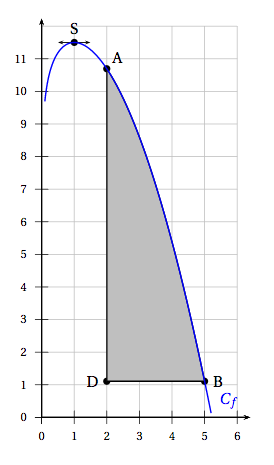
$C_f$ est la représentation graphique de la fonction $f$ définie sur $[0,1~;~+\infty[$ par : $$f(x) = 12+ax^2+\ln(x).$$ où $a$ est un nombre réel qui sera déterminé dans la partie A. S est le point de $C_f$ d’abscisse 1. A est le point de $C_f$ d’abscisse 2. B est le point de $C_f$ d’abscisse 5. D est le point d’intersection de la droite d’équation $x = 2$ et de la droite parallèle à l’axe des abscisses passant par B. La voile est représentée par le domaine délimité par le segment [AD], le segment [DB] et la courbe $C_f$.

Partie A

La fonction $f'$ désigne la fonction dérivée de $f$.

1. On suppose que la tangente à la courbe $C_f$ au point S est horizontale. Que vaut $f'(1)$ ?
La tangente à la courbe $C_f$ au point S d'abscisse 1 est horizontale donc $f′⁡(1)=0$.
2. Calculer $f'(x)$ pour tout réel $x$ de $[0,1~;~+\infty[$.
$f′$ est la fonction définie pour tout réel $x$ de l'intervalle $[0,1~;~+\infty[$ par $f′⁡(x)=2⁢a⁢x+\dfrac{1}{x}$.
3. 1. Exprimer $f'(1)$ en fonction de $a$.
   $f′⁡(1)=2⁢a+1.$
   2. Démontrer que $a=-0,5$ .
   $f′⁡(1)=0\iff 2⁢a+1=0\iff a=-0,5$
   Ainsi, $f$ est la fonction définie pour tout réel $x$ de l'intervalle $[0,1~;~+\infty[$ par $f⁡(x)=12-0,5⁢x^2+\ln⁡ x.$

Partie B

1. Montrer que la fonction $F$ définie sur $[0,1~;~+\infty[$ par $$F(x)=11x-\frac{1}{6}x^3 + x\ln(x)$$ est une primitive de $f$ sur $[0,1~;~+\infty[$.
2. 1. Calculer la valeur exacte, exprimée en unité d’aire, de l’aire du domaine limité par la courbe $C_f$, l’axe des abscisses et les droites d’équation $x=2$ et $x=5$.
   Étudions le signe de la fonction $f$ sur $[0,1; 5]$.
   Les variations de la fonction $f$ se déduisent du signe de sa dérivée $f′$ définie sur $[0,1~;~+\infty[$ par : $f′⁡(x) =-x+\dfrac{1}{x}=\dfrac{-x^2}{x}+\dfrac{1}{x}= \dfrac{1-x^2}{x}= \dfrac{(1-x)(1+x)}{x}$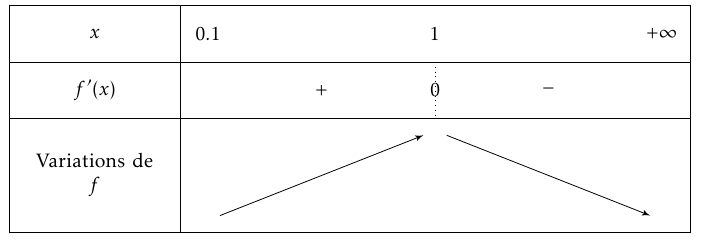
   
   Comme d'autre part, $f⁡(0,1)\approx 9,7, f⁡(1)=11,5$ et $f⁡(5)\approx 1,1$ on en déduit que sur l'intervalle $[0,1; 5]$ on a $f⁡(x)>0$.
   Calcul de l'aire :
   Sur l'intervalle $[0,1; 5]$ la fonction $f$ est positive par conséquent l'aire, exprimée en unité d'aire, du domaine limité par la courbe $C_f$, l'axe des abscisses et les droites d'équation $x=2$ et $x=5$ est égale à : $$\begin{array}{rl} \displaystyle\int_2^5 f(x)\; dx & = F(5)-F(2)\\ &= 55- \frac{125}{6}+5\ln5-22-\frac{8}{6}+2\ln2\\ &=\frac{27}{2}+5\ln5-2\ln2 \end{array}$$
   L’aire du domaine limité par la courbe $C_f$, l'axe des abscisses et les droites d'équation $x=2$ et $x=5$ est égale à $\dfrac{27}{2}+5⁢\ln⁡ 5-2\ln 2$ unités d'aire.
   2. Vérifier qu’une valeur approchée de cette aire, arrondie au dixième, est $20,2$ m $^2$.
   L'unité d'aire est égale à un mètre carré et $\dfrac{27}{2}+5⁢\ln⁡ 5-2\ln 2\approx 20,16$ d'où :
   La valeur arrondie au dixième près de l'aire du domaine limité par la courbe $C_f$, l'axe des abscisses et les droites d'équation x=2 et x=5 est 20,2 m$^2$.
3. Cette voile doit être légère tout en étant suffisamment résistante. Elle est fabriquée dans un tissu ayant une masse de $260$ grammes par mètre carré. La voile pèsera-t-elle moins de $5$ kg ? Justifier la réponse.
L'aire en mètre carré de la voile est égale à l'aire de la partie grisée soit : $$\begin{array}{rl} \displaystyle\int_2^5 f(x)\; dx -DB\times f(5) & =\frac{27}{2}+5\ln5-2\ln2 -3\times \left( -\frac{1}{2} +\ln 5\right) \\ &= \frac{27}{2}+5\ln5-2\ln2 +\frac{3}{2} -3\ln 5 \\ &=15-2\ln2 -3\ln 5 \\ &= 15-2\left( \ln 2-\ln 5 \right) \\ &= 15-2\ln\left( \frac{5}{2}\right) \\ &=15-2\ln\left( 2,5\right) \\ \end{array}$$ La masse de la voile en kilogramme est donc égale à $0,26\times \left( 15-2\ln\left( 2,5\right) \right) \approx 4,376$
La masse de la voile est inférieure à 5 kg.