Baccalauréat STI2D Antilles Guyane 2013

Exercice 1 4 points

Suites

1. L'algorithme ci-dessous permet de calculer les termes successifs d'une suite que l'on appellera $\left(u_{n}\right)$. $$\begin{array}{|ll|}\hline \text{Entrée} :&\text{ Saisir la valeur de l'entier naturel } n\\ \text{Traitement} :&\text{ Affecter 2 à la variable } u \\ &\text{ Pour } i\text{ variant de 1 à } n \\ &\hspace{1cm}\text{ Affecter } 1,5u \text{ à }u \\ &\text{ Fin de Pour }\\ \text{Sortie} :& \text{Afficher } u\\ \hline \end{array}$$ Quelles valeurs affiche cet algorithme lorsque l'on saisit $n = 1$, puis $n = 2$ et enfin $n = 3$ ?
2. On considère la suite $\left(u_{n}\right)$ définie par $u_{0} = 2$ et, pour tout entier naturel $n$, $u_{n+1} = 1,5 u_{n}$.
   1. Quelle est la nature de la suite $\left(u_{n}\right)$ ? Préciser ses éléments caractéristiques.
   2. Pour tout entier naturel $n$, donner l'expression du terme $u_{n}$ en fonction de $n$.
3. On considère la suite $\left(S_{n}\right)$ définie pour tout entier naturel $n$ par : \[S_{n} = \displaystyle\sum_{k=0}^n u_{k} = u_{0} + u_{1} + u_{2} + \ldots + u_{n}.\]
   1. Calculer les valeurs des termes $S_{0}$, $S_{1}$ et $S_{2}$.
   2. Quelles modifications doit-on faire à l'algorithme précédent pour qu'il affiche la valeur du terme $S_{n}$ pour un $n$ donné ? Écrire ce nouvel algorithme sur sa copie.
   3. Calculer le terme $S_{n}$ en fonction de l'entier naturel $n$.
   4. En déduire la limite de la suite $\left(S_{n}\right)$.

Correction de l'exercice 1 (4 points)

Suites

1. L'algorithme ci-dessous permet de calculer les termes successifs d'une suite que l'on appellera $\left(u_{n}\right)$. $$\begin{array}{|ll|}\hline \text{Entrée} :&\text{ Saisir la valeur de l'entier naturel } n\\ \text{Traitement} :&\text{ Affecter 2 à la variable } u \\ &\text{ Pour } i\text{ variant de 1 à } n \\ &\hspace{1cm}\text{ Affecter } 1,5u \text{ à }u \\ &\text{ Fin de Pour }\\ \text{Sortie} :& \text{Afficher } u\\ \hline \end{array}$$ Quelles valeurs affiche cet algorithme lorsque l'on saisit $n = 1$, puis $n = 2$ et enfin $n = 3$ ?
   • Pour $n = 1$, l'algorithme affiche $u_{1} = 2 \times 1,5 = 3$.
   • Pour $n = 2$, l'algorithme affiche $u_{2} = 3 \times 1,5 = 4,5$.
   • Pour $n = 3$, l'algorithme affiche $u_{3} = 4,5 \times 1,5 = 6,75$.
2. On considère la suite $\left(u_{n}\right)$ définie par $u_{0} = 2$ et, pour tout entier naturel $n$, $u_{n+1} = 1,5 u_{n}$.
   1. Quelle est la nature de la suite $\left(u_{n}\right)$ ? Préciser ses éléments caractéristiques.
   D'après la définition, $\left(u_{n}\right)$ est une suite géométrique de raison $q = 1,5$ et de premier terme $u_{0} = 2$.
   2. Pour tout entier naturel $n$, donner l'expression du terme $u_{n}$ en fonction de $n$.
   On sait que pour tout naturel $n$, \: $u_{n} = u_{0}\times q^n = 2 \times 1,5^n$.
3. On considère la suite $\left(S_{n}\right)$ définie pour tout entier naturel $n$ par : \[S_{n} = \displaystyle\sum_{k=0}^n u_{k} = u_{0} + u_{1} + u_{2} + \ldots + u_{n}.\]
   1. Calculer les valeurs des termes $S_{0}$, $S_{1}$ et $S_{2}$.
      • $ = u_{0} = 2$ ;
      • $S_{1} = u_{0} + u_{1} = S_{0}+ u_{1}=2 + 3 = 5$ ;
      • $S_{2} = u_{0} + u_{1} + u_{2} = S_{1}+ u_{2}= 5 + 4,5 = 9,5$.
   2. Quelles modifications doit-on faire à l'algorithme précédent pour qu'il affiche la valeur du terme $S_{n}$ pour un $n$ donné ? Écrire ce nouvel algorithme sur sa copie.
   $$\begin{array}{|ll|}\hline \text{Entrée} :&\text{ Saisir la valeur de l'entier naturel } n\\ \text{Traitement} :&\text{ Affecter 2 à la variable } u \\ &\text{ Affecter 2 à la variable } S \\ &\text{ Pour } i\text{ variant de 1 à } n \\ &\hspace{1cm}\text{ Affecter } 1,5u \text{ à }u \\ &\hspace{1cm}\text{ Affecter } S+u \text{ à } S \\ &\text{ Fin de Pour }\\ \text{Sortie} :& \text{Afficher } S\\ \hline \end{array}$$
   3. Calculer le terme $S_{n}$ en fonction de l'entier naturel $n$.
   $$\begin{array}{ll}S_{n} &= \displaystyle\sum_{k = 0}^n u_{k} \\ &= u_{0} \times\dfrac{1 - q^{n+1}}{1 - q}\\& = 2 \times \dfrac{1 - 1,5^{n+1}}{1 - 1,5} \\&= 2 \times \dfrac{1,5^{n+1} - 1}{1,5 - 1}\\& = 4\left(1,5^{n+1} - 1\right)\\& =S_{n}\\& = 6 \times 1,5^n - 4\end{array}$$
   $S_{n} = 6 \times 1,5^n - 4$
   4. En déduire la limite de la suite $\left(S_{n}\right)$.
   Comme $1,5 > 1$, on sait que $\displaystyle\lim_{n \to +\infty} 1,5^n = + \infty$, donc $\displaystyle\lim_{n \to +\infty} S_{n} = + \infty$.

Exercice 2 5 points

Probabilités

Une entreprise spécialisée produit des boules de forme sphérique pour la compétition. Le responsable de la qualité cherche à analyser la production. Il mesure pour cela la masse des boules d'un échantillon (E) de 50 pièces de la production concernée, et obtient les résultats suivants pour la série statistique des masses : $$ \begin{array}{|l|l|l|l|l|l|l|l|l|l|}\hline \text{ Masse en } g &1195 &1196 &1197 &1198 &1199 &1200 &1201 & 1202 &1203 &1204 \\ \hline \text{ Nombre de boules } &1 &3 &4 &6 &8 &11 &6 &5 &3 &3\\ \hline \end{array}$$ Une boule est dite « de bonne qualité » si sa masse en grammes $m$ vérifie : $1197 \leqslant m \leqslant 1203 $.

1. 1. Calculer, pour l'échantillon (E), le pourcentage de boules de bonne qualité.
   2. Déterminer la moyenne et l'écart type de la série des masses de cet échantillon. (On donnera des valeurs approchées au gramme près.)
   Dans la suite de l'exercice, on admet que la probabilité qu'une boule soit de bonne qualité est : $p = 0,86$. Les résultats des différentes probabilités seront donnés au millième près.
2. L'entreprise livre des lots de boules à un client. On assimile le choix de chaque pièce d'un lot à un tirage avec remise. On désigne par $X$ la variable aléatoire qui, à un lot donné de 50 boules, associe le nombre de boules de bonne qualité.
   1. Justifier que $X$ suit une loi binomiale dont on précisera les paramètres $n$ et $p$.
   2. Déterminer la probabilité qu'il y ait au moins 48 boules de bonne qualité dans le lot.
3. On décide d'approcher la loi binomiale suivie par la variable aléatoire $X$ par une loi normale d'espérance $m$ et d'écart type $\sigma$.
   1. Justifier que $m = 43$ et $\sigma \approx 2,45$.
   2. Déterminer, à l'aide de cette loi normale, une approximation de la probabilité qu'il y ait au moins 48 boules de bonne qualité dans le lot.
4. Le client reçoit un lot de 50 boules.
   1. Préciser l'intervalle de fluctuation asymptotique à 95$\,\%$ de la fréquence des boules de bonne qualité pour un lot de 50 pièces.
   2. Dans son lot, le client a 42 boules qui sont de bonne qualité. Il affirme au fabricant que la proportion de boules de bonne qualité est trop faible au regard de la production habituelle de l'entreprise. Peut-on donner raison au client au seuil de confiance de 95 $\,\%$ ? Justifier.

Correction de l'exercice 2 (5 points)

Probabilités

Une entreprise spécialisée produit des boules de forme sphérique pour la compétition. Le responsable de la qualité cherche à analyser la production. Il mesure pour cela la masse des boules d'un échantillon (E) de 50 pièces de la production concernée, et obtient les résultats suivants pour la série statistique des masses : $$ \begin{array}{|l|l|l|l|l|l|l|l|l|l|}\hline \text{ Masse en } g &1195 &1196 &1197 &1198 &1199 &1200 &1201 & 1202 &1203 &1204 \\ \hline \text{ Nombre de boules } &1 &3 &4 &6 &8 &11 &6 &5 &3 &3\\ \hline \end{array}$$ Une boule est dite « de bonne qualité » si sa masse en grammes $m$ vérifie : $1197 \leqslant m \leqslant 1203 $.

1. 1. Calculer, pour l'échantillon (E), le pourcentage de boules de bonne qualité.
   Il y a $1 + 3 + 3 = 7$ boules dont la masse n'appartient pas à l'intervalle $[ 1197 ~;~ 1203 ]$.
   Il y a donc $50 - 7 = 43$ boules de « de bonne qualité » sur 50 soit $\dfrac{43}{50} = \dfrac{86}{100} = 0,86 = 86\,\%$.
   Pour l'échantillon (E), il y a $86\,\%$ de boules de bonne qualité
   2. Déterminer la moyenne et l'écart type de la série des masses de cet échantillon. (On donnera des valeurs approchées au gramme près.)
   La moyenne : $\overline{m} = \dfrac{1 \times 1195 + 3 \times 1196 + \ldots 3 \times1204}{50} = 1199,76 \approx 1200$~(g).
   Pour l'écart-type $\sigma$, la calculatrice donne $\sigma \approx 2$.
   Dans la suite de l'exercice, on admet que la probabilité qu'une boule soit de bonne qualité est : $p = 0,86$. Les résultats des différentes probabilités seront donnés au millième près.
2. L'entreprise livre des lots de boules à un client. On assimile le choix de chaque pièce d'un lot à un tirage avec remise. On désigne par $X$ la variable aléatoire qui, à un lot donné de 50 boules, associe le nombre de boules de bonne qualité.
   1. Justifier que $X$ suit une loi binomiale dont on précisera les paramètres $n$ et $p$.

   On répète $\1$  fois, de façon indépendante, l’expérience «\2 » qui comporte 2 issues :

   • « \3 » considéré comme succès, de probabilité $p=\4$
   • « \5 » considéré comme échec, de probabilité $q=1-p=\6$

   Nous sommes donc en présence d’un schéma de Bernoulli et la variable aléatoire $\7$ prenant pour valeurs le nombre de succès obtenus suit la loi binomiale de paramètres $\1$  et $\4$ notée $\mathscr{B}(\1;\4)$ .

   Pour tout entier $k$ où $0\leq k\leq \1$, on a $$P(\7=k)=\binom{\1}{k}\times \left(\4\right)^k\times\left( \6\right)^{\1-k}$$

   2. Déterminer la probabilité qu'il y ait au moins 48 boules de bonne qualité dans le lot.
   • Méthode 1 : Cette probabilité est égale à $p(X = 48) + p(X = 49) + p(X = 50) \approx 0,01723 + 0,00432 + 0,00053 \approx 0,02208 \approx 0,022$.
     Par exemple pour $p(X=48)$:
     

     2ND DISTR 0binomFdP( \1 , \2,\3)EXE
     Avec une calculatrice de type TI $binomFdP(\1,\2,\3) \approx \4$

     $$P( \5 = \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
   • Méthode 2 : On passe par l'événement contraire : $p(X\geq 48)=1-p(X\leq 47)$
     

      

     2ND DISTR AbinomFRép( \1 , \2,\3)EXE
     Avec une calculatrice de type TI $$binomFR\text{é}p(\1,\2,\3) \approx \4$$

     $$P( \5 \leq \3)\approx \4 \text{ à } 10^{-\6} \text{ près.}$$
     
     Donc $p(X\geq 48)=1-p(X\leq 47)\approx 1-0,9779\approx 0,022$
3. On décide d'approcher la loi binomiale suivie par la variable aléatoire $X$ par une loi normale d'espérance $m$ et d'écart type $\sigma$.
   1. Justifier que $m = 43$ et $\sigma \approx 2,45$.
   $X$ suit la loi binomiale de paramètres $n = 50$ et $p = 0,86$, donc $m = 50 \times 0,86 = 43$ et $\sigma = \sqrt{50 \times 0,86 \times (1 ) 0,86)} = \sqrt{6,02} \approx 2,453 \approx 2,45$.
   2. Déterminer, à l'aide de cette loi normale, une approximation de la probabilité qu'il y ait au moins 48 boules de bonne qualité dans le lot.
4. Le client reçoit un lot de 50 boules.
   1. Préciser l'intervalle de fluctuation asymptotique à 95$\,\%$ de la fréquence des boules de bonne qualité pour un lot de 50 pièces.

   La proportion $p$ est égale à  $\1$. La taille  $n$  de l'échantillon considéré est égale à  $\2.$
   Comme  $ n =\2$ ,   $n \times p  $=\3  et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.

   En effet on a bien : $$n \geq 30\;;\; n \times p \geq 5 \text{ et } n\times (1-p) \geq 5$$

   
   L'intervalle de fluctuation asymptotique au seuil de  $95\% $  est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$ 

   L'intervalle de fluctuation asymptotique à 95 $\,\%$ de la fréquence des boules de bonne qualité pour un lot de $50$~pièces est égal à : $$I_{50} = \approx [0,764~;~0,956]$$
   2. Dans son lot, le client a 42 boules qui sont de bonne qualité. Il affirme au fabricant que la proportion de boules de bonne qualité est trop faible au regard de la production habituelle de l'entreprise. Peut-on donner raison au client au seuil de confiance de 95 $\,\%$ ? Justifier.
   On vérifie que : $n = 50 \quad ; \quad np = 50 \times 0,86 = 43 \quad ; \quad n(1 - p) = 50 \times 0,14 = 7$. Toutes les conditions sont réunies et il y a 42 boules de bonne qualité sur 50 soit une fréquence $f = \dfrac{42}{50} = 0,84$.
   Comme $0,84 \in [0,764~;~0,956]$, on peut dire au seuil de confiance de 95 $\,\%$ que 86$\,\%$ des boules sont de bonne qualité.

Exercice 3 5 points

Nombres complexes

Le plan complexe est rapporté à un repère orthonormal direct $\left( {{\mathrm{O}};\vec u,\vec v} \right)$. On note $\mathbb C$ l'ensemble des nombres complexes, et i le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$. \bigskip

1. On considère l'équation (E) d'inconnue $z$ : \[(2 - \mathrm{i})z = 2 - 6\mathrm{i}.\]
   1. Résoudre dans $\mathbb C$ l'équation (E). On notera $z_{1}$ la solution de (E) que l'on écrira sous forme algébrique.
   2. Déterminer la forme exponentielle de $z_{1}$.
   3. Soit $z_{2}$ le nombre complexe défini par : $z_{2} = e^{- \mathrm{i}\frac{\pi}{2}} \times z_{1}$. Déterminer les formes exponentielle et algébrique de $z_{2}$.
2. Soit $A$, $B$ et $C$ les points du plan d'affixes respectives : $z_{A} = 2 - 2\mathrm{i}$, $z_{B} = - 2 - 2\mathrm{i}$ et $z_{C} = - 4\mathrm{i}$.
   1. Placer les points $A$, $B$ et $C$ dans le plan complexe.
   2. Calculer le produit scalaire $\vec{CA} \cdot \vec{CB}$.
   3. Déterminer la nature du triangle $ABC$.

Correction de l'exercice 3 (5 points)

Nombres complexes

Le plan complexe est rapporté à un repère orthonormal direct $\left( {{\mathrm{O}};\vec u,\vec v} \right)$. On note $\mathbb C$ l'ensemble des nombres complexes, et i le nombre complexe de module 1 et d'argument $\dfrac{\pi}{2}$.

1. On considère l'équation (E) d'inconnue $z$ : \[(2 - i)z = 2 - 6i.\]
   1. Résoudre dans $\mathbb C$ l'équation (E). On notera $z_{1}$ la solution de (E) que l'on écrira sous forme algébrique.
   Rappel : Pour calculer le quotient de deux nombres complexes, on multiplie numérateur et dénominateur par le conjugué du dénominateur. $$\begin{array}{lll} (2 - i)z = 2 - 6i&\iff z = \dfrac{2-6i}{2-i}&\\ &\iff z = \dfrac{(2-6i)(2+i)}{(2-i)(2+i)}& \\ &\iff z = \dfrac{4+2i-12i+6}{2^2+1^2}& \text{ car } z\overline{z}=a^2+b^2\\ &\iff z = \dfrac{10-10i}{5}& \\ &\iff z = 2-2i &\\ \end{array}$$
   L'équation (E) a pour ensemble de solution : $\mathcal{S}=\{2-2i\}$
   2. Déterminer la forme exponentielle de $z_{1}$.
   Forme trigonométrique de $z_1=2-2i$:
   Module : $|z_1|=\sqrt{a^2+b^2}=\sqrt{2^2+2^2}=\sqrt{8}=2\sqrt{2}$
   Argument: $$\left\{ \begin{array}{l } \cos(\theta)=\dfrac{a}{r}= \dfrac{2}{2\sqrt{2}}= \dfrac{1}{ \sqrt{2}}= \dfrac{\sqrt2}{ 2}\\ \sin(\theta)=\dfrac{b}{r}= \dfrac{-2}{2\sqrt{2}}=-\dfrac{\sqrt2}{ 2} \end{array} \right.$$ Ainsi $\theta=-\dfrac{\pi}{4}$ convient; on a donc: $$z_1=[2\sqrt{2};-\dfrac{\pi}{4}] \text{ ou } z_2=2\sqrt{2}\left [\cos\left (-\dfrac{\pi}{4}\right )+i\sin\left (-\dfrac{\pi}{4}\right )\right ]$$
   La forme exponentielle de $z_{1}$ est $z_1= 2\sqrt{2}e^{-i\frac{\pi}{4}}$
   3. Soit $z_{2}$ le nombre complexe défini par : $z_{2} = e^{- i\frac{\pi}{2}} \times z_{1}$. Déterminer les formes exponentielle et algébrique de $z_{2}$.
2. Soit $A$, $B$ et $C$ les points du plan d'affixes respectives : $z_{A} = 2 - 2i$, $z_{B} = - 2 - 2i$ et $z_{C} = - 4i$.
   1. Placer les points $A$, $B$ et $C$ dans le plan complexe.
   
   2. Calculer le produit scalaire $\vec{CA} \cdot \vec{CB}$.
      • Le vecteur $\vec{CA}$ a pour affixe $z_{\vec{CA}}=z_A-z_C=2-2i-(-4i)= 2-2i+4i= 2+2i$ donc $\vec{CA}$ a pour coordonnées $\begin{pmatrix} 2 \\ 2 \end{pmatrix}$
      • Le vecteur $\vec{CB}$ a pour affixe $z_{\vec{CB}}=z_B-z_C=2-2i-(-4i)= -2-2i+4i= -2+2i$ donc $\vec{CB}$ a pour coordonnées $\begin{pmatrix} -2 \\ 2 \end{pmatrix}$
      • $\vec{CA} \cdot \vec{CB} = XX'+YY' = 2 \times (-2) + 2\times 2 =-4 + 4 +0$
      $\vec{CA} \cdot \vec{CB} =0$, ce qui montre que les vecteurs $\vec{CA}$ et $ \vec{CB}$ sont orthogonaux et donc le triangle $ABC$ est rectangle en $C$.
   3. Déterminer la nature du triangle $ABC$.
   On sait déjà que $ABC$ est rectangle en $C$ ;
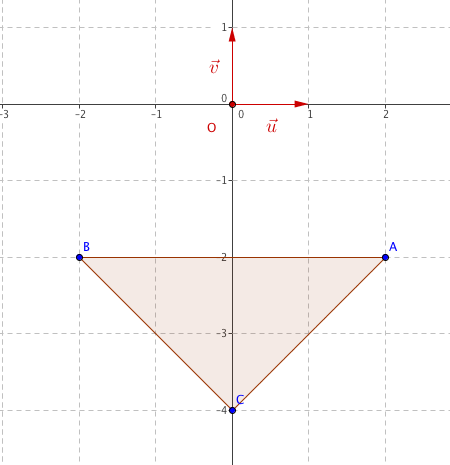
   $CA =\vert z_A-z_C\vert =\vert 2+2i \vert =\sqrt{2^2+2^2}= \sqrt 8 = 2\sqrt 2$
   $CB =\vert z_B-z_C\vert =\vert -2+2i \vert =\sqrt{2^2+2^2}= \sqrt 8 = 2\sqrt 2$
   Ayant $CA=CB$ , le triangle $ABC$ est rectangle isocèle en $C$.
   Le triangle $ABC$ est rectangle isocèle en $C$.

Exercice 4 6 points

Fonctions logarithmes

Soit $f$ la fonction définie sur $]0~;~+ \infty[$ par $f(x) = \dfrac{1}{x} - \ln x$. On appelle $\mathcal{C}_{f}$ sa courbe représentative dans un repère orthonormal $\left( {{\mathrm{O}};\vec i,\vec j} \right)$.

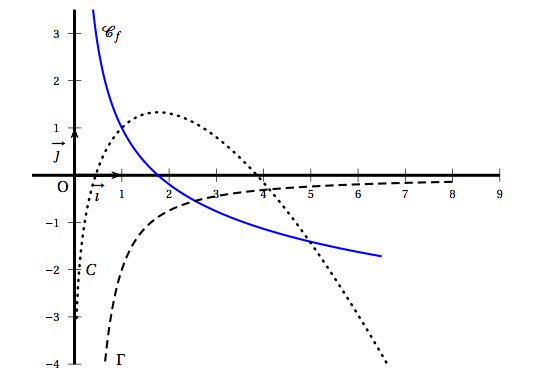
1. Sur le graphique ci-dessous, on donne $\mathcal{C}_{f}$ et les courbes $C$ et $\Gamma$. L'une de ces deux courbes représente graphiquement la dérivée $f'$ de $f$, et l'autre une des primitives $F$ de $f$.
   1. Indiquer laquelle des deux courbes $C$ et $\Gamma$ représente graphiquement $f'$. Justifier.
   2. Par lecture graphique, donner $F(1)$.
   
2. Dans cette question, on pourra vérifier la cohérence des résultats obtenus avec les courbes représentatives données sur le dessin.
   1. Déterminer la limite de la fonction $f$ quand $x$ tend vers $0$. Interpréter graphiquement cette limite.
   2. Déterminer la limite de la fonction $f$ quand $x$ tend vers $+ \infty$.
   3. Calculer $f'(x)$ et montrer que l'on peut écrire : $f'(x) = \dfrac{- x - 1}{x^2}$.
   4. Étudier le signe de $f'(x)$ puis donner le tableau de variations de $f$.
3. Soit $H$ la fonction définie sur $]0~;~+ \infty[$ par $H(x) = x - (x - 1) \ln x$.
   1. Montrer que $H$ est une primitive de $f$ sur $]0~;~+ \infty[$.
   2. En déduire l'expression de la fonction $F$ de la question 1.
   3. Calculer $\displaystyle\int_{1}^{e} f(x)\:\mathrm{d}x$.

Exercice 4 6 points

Fonctions logarithmes

Soit $f$ la fonction définie sur $]0~;~+ \infty[$ par $f(x) = \dfrac{1}{x} - \ln x$. On appelle $\mathcal{C}_{f}$ sa courbe représentative dans un repère orthonormal $\left( {{\mathrm{O}};\vec i,\vec j} \right)$.

1. Sur le graphique ci-dessous, on donne $\mathcal{C}_{f}$ et les courbes $C$ et $\Gamma$. L'une de ces deux courbes représente graphiquement la dérivée $f'$ de $f$, et l'autre une des primitives $F$ de $f$.
   1. Indiquer laquelle des deux courbes $C$ et $\Gamma$ représente graphiquement $f'$. Justifier.
   Sur le graphique on voit que $f$ est décroissante sur $]0~;~+ \infty[$ ; donc sur cet intervalle $f'(x) < 0$ : seuls les points de $\Gamma$ ont tous leurs ordonnées négatives .
   $\Gamma$ est donc la représentation de $f'$.
   2. Par lecture graphique, donner $F(1)$.
   D'après la question précédente $C$ est la représentation graphique de l'une des primitives de $f$. On lit sur le graphe que le point de $C$ d'abscisse 1 a pour ordonnée 1. $F(1) = 1$.
   
2. Dans cette question, on pourra vérifier la cohérence des résultats obtenus avec les courbes représentatives données sur le dessin.
   1. Déterminer la limite de la fonction $f$ quand $x$ tend vers $0$. Interpréter graphiquement cette limite.
   On a pour $x > 0 , \: \displaystyle\lim_{x \to 0} \dfrac{1}{x} = + \infty$ et $\displaystyle\lim_{x \to 0} \ln x = - \infty$, donc par différence $\displaystyle\lim_{x \to 0} \dfrac{1}{x} - \ln x = + \infty$. Graphiquement ceci signifie que l'axe des ordonnées est asymptote verticale au graphe de $f$.
   2. Déterminer la limite de la fonction $f$ quand $x$ tend vers $+ \infty$.
   $\displaystyle\lim_{x \to + \infty} \dfrac{1}{x} = 0$ et $\displaystyle\lim_{x \to + \infty} - \ln x = - \infty$, donc par somme de limites, $\displaystyle\lim_{x \to + \infty} f(x) = - \infty$.
   3. Calculer $f'(x)$ et montrer que l'on peut écrire : $f'(x) = \dfrac{- x - 1}{x^2}$.
   Sur $]0~;~+ \infty[$, \:$f$ est dérivable et $f'(x) = - \dfrac{1}{x^2} - \dfrac{1}{x} = \dfrac{- 1 - x}{x^2} = - \dfrac{x + 1}{x^2} = \dfrac{- x - 1}{x^2}$.
   4. Étudier le signe de $f'(x)$ puis donner le tableau de variations de $f$.
   Comme $x^2 > 0$ pour $x > 0$, le signe de $f'(x)$ est celui du numérateur $- x - 1$.
   $- x - 1 > 0 \iff - 1 > x \iff x < - 1$
   et $- x - 1 < 0 \iff - 1 < x \iff x > - 1$.
   Comme $x > 0$, la dérivée est donc négative et ceci confirme que la fonction $f$ est décroissante sur $]0~;~+ \infty[$. D'où le tableau de variations :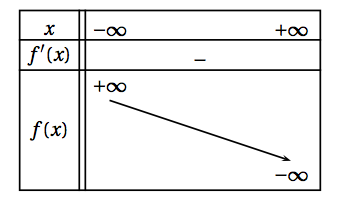
   
3. Soit $H$ la fonction définie sur $]0~;~+ \infty[$ par $H(x) = x - (x - 1) \ln x$.
   1. Montrer que $H$ est une primitive de $f$ sur $]0~;~+ \infty[$.
   On a $H'(x) = 1 - 1\ln x - (x - 1) \times \dfrac{1}{x} = 1 - \ln x - 1 + \dfrac{1}{x} = \dfrac{1}{x} - \ln x = f(x).$ $H$ est donc une des primitives de $f$.
   2. En déduire l'expression de la fonction $F$ de la question 1.
   On a $H(1) = \dfrac{1}{1} - \ln 1 = 1$ et on a vu que $F(1) = 1$, donc $F = H$ et $F(x) = x - (x - 1) \ln x$.
   3. Calculer $\displaystyle\int_{1}^{e} f(x)\:\mathrm{d}x$.
   On connaît une primitive de $f$ on peut donc calculer l'intégrale : $$\begin{array}{ll}\displaystyle\int_{1}^{\text{e}} f(x)\:\text{d}x &= \left[F(x) \right]_{0}^{\text{e}}\\& = F(\text{e}) - F(1) \\&= \text{e} - (\text{e} - 1) \ln \text{e} - \left[1 - (1 - 1) \ln 1 \right]\\& = \text{e} - (\text{e} - 1) - 1\\& = 1 - 1 \\&= 0\end{array}$$