Baccalauréat S Métropole 21 juin 2019 - Correction Exercice 2
Exercice 2 5 points
Une plateforme informatique propose deux types de jeux vidéo : un jeu de type A et un jeu de type B.
Partie A
Les durées des parties de type A et de type B, exprimées en minutes, peuvent être modélisées respectivement par deux variables aléatoires notées $X_A$ et $X_B$.
La variable aléatoire $X_A$ suit la loi uniforme sur l’intervalle [9; 25].
La variable aléatoire $X_B$ suit la loi normale de moyenne $\mu$ et d’écart type 3. La représentation graphique de la fonction de densité de cette loi normale et son axe de symétrie sont donnés ci-dessous. 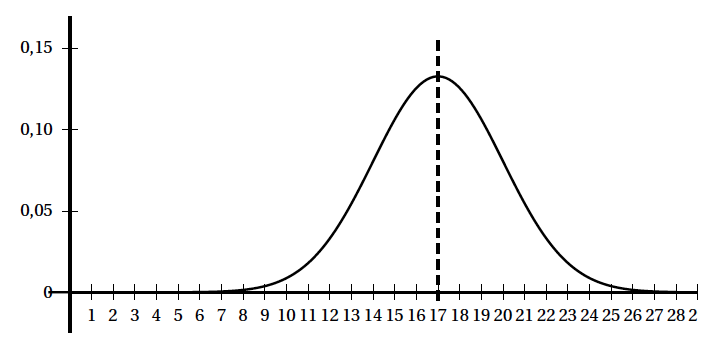
- Calculer la durée moyenne d’une partie de type A. La variable aléatoire $X_A$ suit la loi uniforme sur l’intervalle $[9;25]$ donc $E\left(X_A\right)=\dfrac{9+25}{2}=17$.
- Une partie de type $A$ dure donc en moyenne $17$ minutes.
- $\quad$
- Préciser à l’aide du graphique la durée moyenne d’une partie de type B.
L’axe de symétrie de la représentation graphique de la fonction de densité semble avoir pour équation $x=17$.
- Une partie de type $B$ dure donc en moyenne $17$ minutes également.
- On choisit au hasard, de manière équiprobable, un type de jeu. Quelle est la probabilité que la durée d’une partie soit inférieure à 20 minutes ? On donnera le résultat arrondi au centième. On a $P\left(X_A\leq 20\right)=\dfrac{20-9}{25-9}=0,687~5$.
- $\quad$
- et
- $\begin{align*} P\left(X_B\leq 20\right)&=P\left(X_B\leq 17\right)+P\left(17\leq X_B\leq 20\right) \\
- &=0,5+P\left(17\leq X_B\leq 20\right) \\
- &\approx 0,841~3\end{align*}$
- On choisit de manière équiprobable un type de jeu.
2ND DISTR 2NORMALFRép( -10^(99) , \1,$\2$,$\3$)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(-10^{99},\1,\2,\3) \approx \4$$
- $\begin{align*} p&=\dfrac{1}{2}\left(P\left(X_A\leq 20\right)+P\left(X_B\leq 20\right) \right) \\
- &\approx 0,76\end{align*}$
- $\quad$
Partie B
On admet que, dès que le joueur achève une partie, la plateforme lui propose une nouvelle partie selon le modèle suivant :
- si le joueur achève une partie de type A, la plateforme lui propose de jouer à nouveau une partie de type A avec une probabilité de 0,8 ;
- si le joueur achève une partie de type B, la plateforme lui propose de jouer à nouveau une partie de type B avec une probabilité de 0,7.
Pour tout entier naturel $n$ supérieur ou égal à 1, on note $A_n$ et $B_n$ les évènements :
- $A_n$ : « la n-ième partie est une partie de type $A$. »
- $B_n$ : « la n-ième partie est une partie de type $B$. »
Pour tout entier naturel $n$ supérieur ou égal à 1, on note $a_n$ la probabilité de l’évènement $A_n$.
- Recopier et compléter l’arbre pondéré ci-contre.
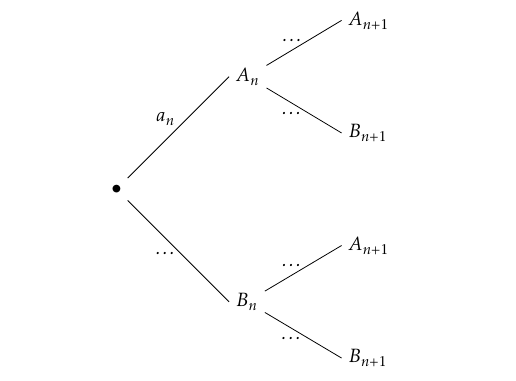
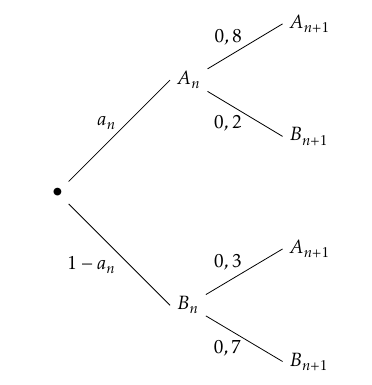
- Montrer que pour tout entier naturel $n> 1$, on a : $$a_{n+1}=0,5a_n=0,3.$$ Pour tout entier naturel $n\geq 1$, d’après la formule des probabilités totales on a :
- $\begin{align*} a_{n+1}&=P\left(A_{n+1}\right) \\
- &=P\left(A_n\cap A_{n+1}\right)+P\left(B_n\cap A_{n+1}\right) \\
- &=0,8a_n+0,3\left(1-a_n\right) \\
- &=0,5a_n+0,3\end{align*}$
- $\quad$
Dans la suite de l’exercice, on note $a$ la probabilité que le joueur joue au jeu $A$ lors de sa première partie, où $a$ est un nombre réel appartenant à l’intervalle [0; 1].- Recopier et compléter l’arbre pondéré ci-contre.
- La suite $\left(a_n\right)$ est donc définie par : $a_1 = a$, et pour tout entier naturel $n > 1, a_{n+1} = 0,5a_n + 0,3$.
- Étude d’un cas particulier : Dans cette question, on suppose que $a = 0,5$.
- Montrer par récurrence que pour tout entier naturel $n > 1$, on a : $0 < a_n < 0,6$.
- si $n=1$ alors $a_1=0,5 \in[0;0,6]$.
- La propriété est vraie au rang $1$.
- $\quad$.
Hérédité :- On suppose la propriété vraie au rang $n$. Donc $0\leq a_n\leq 0,6$.
- Montrons qu’elle est vraie au rang $n+1$, c’est-à-dire que $0\leq a_{n+1}\leq 0,6$.
- $\begin{align*} 0\leq a_n\leq 0,6&\iff 0\leq 0,5a_n\leq 0,3\\
- &\iff 0,3\leq 0,5a_n+0,3\leq 0,6\\
- &\iff 0,3\leq a_{n+1}\leq 0,6\end{align*}$
- Par conséquent $0\leq a_{n+1}\leq 0,6$.
- La propriété est vraie au rang $n+1$.
- $\quad$
Conclusion :- La propriété est vraie au rang $1$ et est héréditaire.
- Par conséquent, pour tout entier naturel $n\geq 1$ on a $0\leq a_n\leq 0,6$.
- $\quad$
- Montrer que la suite $\left(a_n\right)$ est croissante. Pour tout entier naturel $n \geq 1$ :
- $\begin{align*} a_{n+1}-a_n&=0,5a_n+0,3-a_n \\
- &=0,3-0,5a_n \\
- &\geq 0,3-0,5\times 0,6\\
- &\geq 0\end{align*}$
- La suite $\left(a_n\right)$ est donc croissante.
- $\quad$
- Montrer que la suite $\left(a_n\right)$ est convergente et préciser sa limite. La suite $\left(a_n\right)$ est croissante et majorée; elle converge donc vers un réel $\ell$.
- Le réel $\ell$ est solution de l’équation :
- $\ell=0,5\ell+0,3 \iff 0,5\ell=0,3\iff \ell =0,6$.
- La suite $\left(a_n\right)$ converge donc vers $0,6$.
- $\quad$
- Étude du cas général : Dans cette question, le réel $a$ appartient à l’intervalle [0; 1].
On considère la suite $\left(u_n\right)$ définie pour tout entier naturel $n \geq 1$ par : $u_n = a_n - 0,6$.- Montrer que la suite $\left(u_n\right)$ est une suite géométrique. Pour tout entier naturel $n\geq 1$, on a $u_n=a_n-0,6 \iff a_n=u_n+0,6$.
- $\begin{align*} u_{n+1}&=a_{n+1}-0,6\\
- &=0,5a_n+0,3-0,6\\
- &=0,5a_n-0,3\\
- &=0,5\left(u_n+0,6\right)-0,3\\
- &=0,5u_n+0,3-0,3\\
- &=0,5u_n\end{align*}$
- La suite $\left(u_n\right)$ est donc géométrique de raison $0,5$ et de premier terme $u_0=a_0-0,6=a-0,6$.
- $\quad$
- En déduire que pour tout entier naturel $n \geq 1$ on a : $a_n = (a-0,6)\times 0,5^{n-1}+0,6$ . Ainsi, pour tout entier naturel $n\geq 1$ on a $u_n=(a-0,6)\times 0,5^{n-1}$.
- Donc $a_n=u_n+0,6=(a-0,6)\times 0,5^{n-1}+0,6$.
- $\quad$
- Déterminer la limite de la suite $\left(a_n\right)$. Cette limite dépend-elle de la valeur de $a$ ? $-1<0,5<1$ donc $\lim\limits_{n\to +\infty} 0,5^{n-1}=0$ et $\lim\limits_{n\to +\infty} a_n=0,6$.
- Cette limite ne dépend donc pas de $a$.
- $\quad$
- La plateforme diffuse une publicité insérée en début des parties de type A et une autre publicité insérée en début des parties de type B. Quelle devrait être la publicité la plus vue par un joueur s’adonnant intensivement aux jeux vidéo ? Sur le long terme, la probabilité que le joueur fasse une partie de type A est égale à $0,6$ et celle qu’il fasse une partie de type B est égale à $0,4$.
- Il verra donc plus souvent la publicité insérée au début des parties de type A.
- $\quad$
- Vues: 64956