Baccalauréat S Amérique du Sud 21 novembre 2017 - Exercice 2

Page 3 sur 12: Exercice 2

Exercice 2 (4 points)

Commun à tous les candidats

On considère un cube ABCDEFGH.

1. 1. Simplifier le vecteur $\vec{\text{AC}} + \vec{\text{AE}}$.
   2. En déduire que $\vec{\text{AG}}~\cdot~\vec{\text{BD}} = 0$.
   3. On admet que $\vec{\text{AG}}~\cdot~\vec{\text{BE}} = 0$. Démontrer que la droite (AG) est orthogonale au plan (BDE).

   

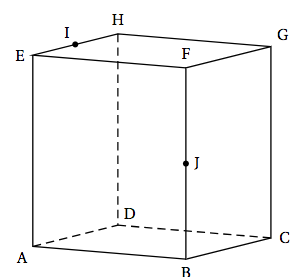
2. L'espace est muni du repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}},~\vec{\text{AE}}\right)$.
   1. Démontrer qu'une équation cartésienne du plan (BDE) est $x + y + z - 1 = 0$.
   2. Déterminer les coordonnées du point d'intersection K de la droite (AG) et du plan (BDE).
   3. On admet que l'aire, en unité d'aire, du triangle BDE est égale à $\dfrac{\sqrt{3}}{2}$. Calculer le volume de la pyramide BDEG.