Baccalauréat S Métropole 20 juin 2013 - Exercice 2

Page 3 sur 10: Exercice 2

Exercice 2 7 points

Commun à tous les candidats

Sur le graphique ci-dessous, on a tracé, dans le plan muni d'un repère orthonormé $\left(\text{O}, \vec{i}, \vec{j}\right)$, la courbe représentative $\mathcal{C}$ d'une fonction $f$ définie et dérivable sur l'intervalle $] 0 ; + \infty[$.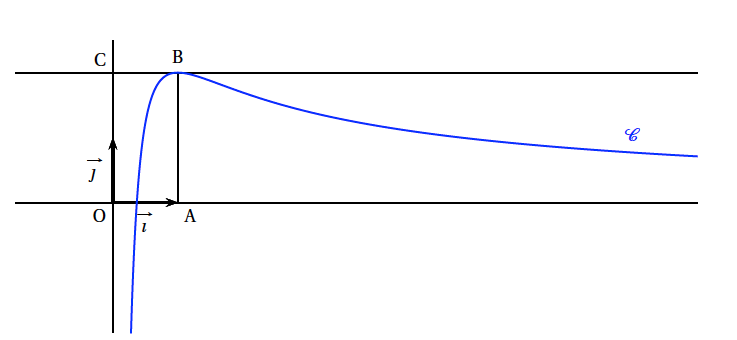

On dispose des informations suivantes :

• les points A, B, C ont pour coordonnées respectives (1, 0), (1, 2), (0, 2);
• la courbe $\mathcal{C}$ passe par le point B et la droite (BC) est tangente à $\mathcal{C}$ en B;
• il existe deux réels positifs $a$ et $b$ tels que pour tout réel strictement positif $x$,

\[f(x) = \dfrac{a+ b\ln x}{x}. \]

1. 1. En utilisant le graphique, donner les valeurs de $f(1)$ et $f'(1)$.
   2. Vérifier que pour tout réel strictement positif $x,\: f'(x) = \dfrac{(b - a) - b \ln x}{x^2}$.
   3. En déduire les réels $a$ et $b$.
2. 1. Justifier que pour tout réel $x$ appartenant à l'intervalle $]0\,, +\infty[,\: f'(x)$ a le même signe que $- \ln x$.
   2. Déterminer les limites de $f$ en 0 et en $+ \infty$. On pourra remarquer que pour tout réel $x$ strictement positif, $f(x) = \dfrac{2}{x} + 2\;\dfrac{\ln x}{x}$.
   3. En déduire le tableau de variations de la fonction $f$.
3. 1. Démontrer que l'équation $f(x) = 1$ admet une unique solution $\alpha$ sur l'intervalle $]0\,, 1]$.
   2. Par un raisonnement analogue, on démontre qu'il existe un unique réel $\beta$ de l'intervalle $]1\,, + \infty]$ tel que $f(\beta) = 1$. Déterminer l'entier $n$ tel que $n < \beta < n + 1$.
4. On donne l'algorithme ci-dessous.
   $$\begin{array}{|l l|}\hline \text{Variables : }& a, b \text{ et } m \text{ sont des nombres réels.}\\ \text{Initialisation :}& \text{Affecter à } a \text{ la valeur 0. } \\ & \text{ Affecter à } b \text{ la valeur 1. }\\ \text{Traitement :}& \text{ Tant que } b - a > 0,1\\ &\begin{array}{l|l} &\text{ Affecter à } m \text{ la valeur } \dfrac{1}{2}(a + b).\\ & \text{ Si } f(m) < 1 \text{ alors Affecter à } a \text{ la valeur } m.\\ & \text{Sinon Affecter à } b \text{ la valeur } m.\\ &F \text{ Fin de Si.}\\ \end{array}\\ &\text{ Fin de Tant que.}\\ \text{ Sortie : }& \text{ Afficher } a.\\ & \text{ Afficher } b.\\ \hline \end{array} $$
   1. Faire tourner cet algorithme en complétant le tableau ci-dessous que l'on recopiera sur la copie.
      $$\begin{array}{|c|c|c|c|c|c|}\hline &\text{étape 1 }&\text{étape 2 }&\text{étape 3 }&\text{étape 4 }&\text{étape 5 }\\ \hline a&0&&&&\\ \hline b&1&&&&\\ \hline b - a&&&&&\\ \hline m&&&&&\\ \hline \end{array}$$
   2. Que représentent les valeurs affichées par cet algorithme ?
   3. Modifier l'algorithme ci-dessus pour qu'il affiche les deux bornes d'un encadrement de $\beta$ d'amplitude $10^{-1}$.
5. Le but de cette question est de démontrer que la courbe $\mathcal{C}$ partage le rectangle OABC en deux domaines d'aires égales.
   1. Justifier que cela revient à démontrer que $\displaystyle\int_{\frac{1}{\text{e}}}^1 f(x)\:\text{d}x = 1$.
   2. En remarquant que l'expression de $f(x)$ peut s'écrire $\dfrac{2}{x} + 2 \times \dfrac{1}{x} \times \ln x$, terminer la démonstration.