Baccalauréat S Pondichéry 16 avril 2013 - Exercice 4

Page 9 sur 11: Exercice 4

Exercice 4

Commun à tous les candidats

Dans une entreprise, on s'intéresse à la probabilité\index{probabilité} qu'un salarié soit absent durant une période d'épidémie de grippe.

• Un salarié malade est absent
• La première semaine de travail, le salarié n'est pas malade.
• Si la semaine $n$ le salarié n'est pas malade, il tombe malade la semaine $n + 1$ avec une probabilité égale à $0,04$.
• Si la semaine $n$ le salarié est malade, il reste malade la semaine $n + 1$ avec une probabilité égale à $0,24$. 
  On désigne, pour tout entier naturel $n$ supérieur ou égal à 1, par $E_{n}$ l'évènement « le salarié est absent pour cause de maladie la $n$-ième semaine » .
  On note $p_{n}$ la probabilité de l'évènement $E_{n}$. On a ainsi : $p_{1} = 0$ et, pour tout entier naturel $n$ supérieur ou égal à 1 : $0 \leqslant p_{n} < 1$.
  
  1. 1. Déterminer la valeur de $p_{3}$ à l'aide d'un arbre de probabilité.
     2. Sachant que le salarié a été absent pour cause de maladie la troisième semaine, déterminer la probabilité qu'il ait été aussi absent pour cause de maladie la deuxième semaine.
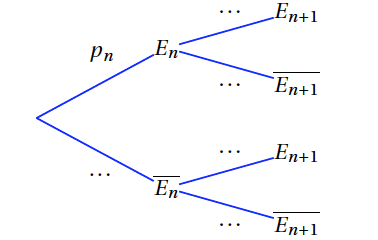
  2. 1. Recopier sur la copie et compléter l'arbre de probabilité donné ci-dessous
     
     
     2. Montrer que, pour tout entier naturel $n$ supérieur ou égal à 1, $p_{n+ 1} = 0,2p_{n} + 0,04$.
     3. Montrer que la suite $\left(u_{n}\right)$ définie pour tout entier naturel $n$ supérieur ou égal à 1 par $u_{n} = p_{n} - 0,05$ est une suite géométrique dont on donnera le premier terme et la raison $r$. En déduire l'expression de $u_{n}$ puis de $p_{n}$ en fonction de $n$ et $r$.
     4. En déduire la limite de la suite $\left(p_{n}\right)$.
     5. On admet dans cette question que la suite $\left(p_{n}\right)$ est croissante. On considère l'algorithme suivant :
        $$\begin{array}{|c|c|}\hline\text{ Variables} & K \text{et}  J \text{sont des entiers naturels,}  P \text{est un nombre réel}\\ \text{Initialisation} & P  \text{prend la valeur}  0\\ &J  \text{prend la valeur}  1\\ \text{Entrée}&\text{ Saisir la valeur de } K\\ \text{Traitement} &\text{Tant que} P < 0,05 - 10^{- \text{K}}\\ &\quad P  \text{prend la valeur}  0,2 \times \text{P} + 0,04\\ &\quad J  \text{prend la valeur} J + 1\\ &\text{Fin tant que }\\ \text{Sortie} &\text{Afficher } J \\ \hline \end{array}$$
        À quoi correspond l'affichage final J ? Pourquoi est-on sûr que cet algorithme s'arrête ?
  3. Cette entreprise emploie 220 salariés. Pour la suite on admet que la probabilité\index{probabilité} pour qu'un salarié soit malade une semaine donnée durant cette période d'épidémie est égale à $p = 0,05$. On suppose que l'état de santé d'un salarié ne dépend pas de l'état de santé de ses collègues. On désigne par $X$ la variable aléatoire qui donne le nombre de salariés malades une semaine donnée.
     1. Justifier que la variable aléatoire $X$ suit une loi binomiale\index{loi binomiale} dont on donnera les paramètres.
        Calculer l'espérance mathématique $\mu$ et l'écart type $\sigma$ de la variable aléatoire $X$.
     2. On admet que l'on peut approcher la loi de la variable aléatoire $\dfrac{X - \mu}{\sigma}$ par la loi normale centrée réduite c'est-à-dire de paramètres $0$ et $1$.
        On note $Z$ une variable aléatoire suivant la loi normale centrée réduite.
        Le tableau suivant donne les probabilités de l'évènement $Z < x$ pour quelques valeurs du nombre réel $x$.
        $$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}\hline x & -1,55 &-1,24 &-0,93 &- 0,62 &- 0,31 &0,00 &0,31 &0,62 &0,93 &1,24 &1,55\\ \hline P(Z < x) & 0,061 &0,108 &0,177 &0,268 &0,379 &0,500 &0,621 &0,732 &0,823 &0,892 &0,939\\ \hline \end{array}$$
        Calculer, au moyen de l'approximation proposée en question b., une valeur approchée à $10^{-2}$ près de la probabilité de l'évènement : « le nombre de salariés absents dans l'entreprise au cours d'une semaine donnée est supérieur ou égal à 7 et inférieur ou égal à 15 » .