Bac STI2D Antilles-Guyane 16 juin 2016 - Exercice 2

Exercice 2 7 points

Fonction exponentielle, calcul intégral

Sur le graphique ci-dessous, $\mathcal{C}$ est la courbe représentative, dans le repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, d'une fonction $f$ définie sur $\mathbb R$.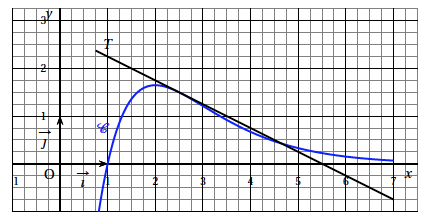

Partie A - Étude graphique

La droite $T$ est tangente à $\mathcal{C}$ au point A(2,5 ; 1,5) et d'ordonnée à l'origine 2,75. L'axe des abscisses est asymptote horizontale à $\mathcal{C}$ au voisinage de $+\infty$. Déterminer graphiquement et indiquer sur votre copie :

1. $f(1)$ ;
2. $f'(2,5)$ ;
3. Une équation de la tangente $T$ ;
4. $\displaystyle\lim_{x\to + \infty} f(x)$.

Partie B - Modélisation

On admet qu'il existe deux réels $a$ et $b$ tels que : $$\text{pour tout réel }\:x,\: \:f(x) = (ax + b)\text{e}^{-x+2,5}.$$

1. Calculer $f'(x)$ en fonction de $a$ et $b$.
2. Exprimer en fonction des réels $a$ et $b$ les nombres suivants : $$f(1) \quad ;\quad f'(2,5).$$
3. Déduire des questions précédentes un système d'équations vérifiées par $a$ et $b$.
4. Résoudre ce système et en déduire l'expression de $f(x)$ en fonction de $x$.

Partie C - Étude algébrique

On admet que pour tout réel $x,\: f(x) = (x - 1)\text{e}^{-x+2,5}$.

1. Déterminer la limite de $f$ en $- \infty$.
2. 1. Montrer que pour tout réel $x$, $$f(x) = \text{e}^{2,5}\left(\dfrac{x}{\text{e}^x} - \dfrac{1}{\text{e}^x}\right).$$
   2. Déterminer la limite de $f$ en $+ \infty$.
3. 1. Calculer $f'(x)$ pour tout réel $x$.
   2. Étudier le signe de $f'$ et en déduire le tableau des variations de la fonction $f$ en faisant figurer les limites trouvées précédemment.

Partie D - Application

On souhaite déterminer l'aire $S$ en unité d'aire de la surface d'une des faces principales du boîtier plastique de l'appareil auditif schématisé ci-contre. Une modélisation mathématique a permis de représenter cette surface.

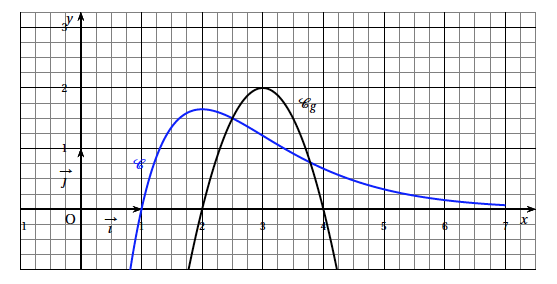
Dans le plan muni du repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, cette surface correspond à la partie du plan limitée par :

• l'axe des abscisses;
• les droites d'équations $x = 1$ et $x = 2,5$ ;
• la courbe représentative $\mathcal{C}$ de la fonction $f$ étudiée précédemment ;
• la courbe représentative $\mathcal{C}_g$ de la fonction $g$ définie par: pour tout réel $x,$ $g(x) = -2x^2 + 12x - 16$.
  
  
  1. Sur l'annexe fournie, hachurer la surface décrite précédemment. Pour déterminer l'aire $S$ de cette surface, on décompose le calcul en deux parties.
  2. Calculer la valeur exacte de l'intégrale suivante : $I = \displaystyle\int_2^{2,5} g(x)\:\text{d}x$.
  3. On souhaite calculer la valeur exacte de l'intégrale suivante : $J = \displaystyle\int_1^{2,5} f(x)\:\text{d}x$ où $f$ est la fonction dont une expression est donnée dans la partie C.
     1. Vérifier qu'une primitive $F$ de la fonction $f$ sur $\mathbb R$ est la fonction définie par : $$\text{pour tout réel }\:x,\: F(x) = - x \text{e}^{-x+2,5}.$$
     2. En déduire la valeur exacte de l'intégrale $J$.
  4. 1. Déterminer la valeur exacte de l'aire $S$ en unité d'aire,
     2. En déduire la valeur arrondie à $10^{-2}$ de l'aire $S$ en unité d'aire.

  Annexe

  
  Page suivante
  Correction Exercice 2
  Page
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • Toutes les pages