Baccalauréat S Métropole 21 juin 2017 - Correction Exercice 1
Page 2 sur 10
Correction de l'exercice 1 (5 points)
Partie A
On considère la fonction $h$ définie sur l’intervalle $[0; +\infty[$ par : $h(x) = x\text{e}^{-x}$.
- Déterminer la limite de la fonction $h$ en $+\infty$. Pour tout réel $x$ on a $h(x)=x\text{e}^{-x}=\dfrac{x}{\text{e}^{x}}=\dfrac{1}{\dfrac{\text{e}^{x}}{x}}$
- Étudier les variations de la fonction $h$ sur l’intervalle $[0; +\infty[$ et dresser son tableau de variations. La fonction $f$ est dérivable sur $[0;+\infty[$ en tant que produit de fonctions dérivables sur cet intervalle.
- L’objectif de cette question est de déterminer une primitive de la fonction $h$.
- Vérifier que pour tout nombre réel $x$ appartenant à l’intervalle $[0; +\infty[$ on a : $h(x) = \text{e}^{-x} — h(x)$ où $h’$ désigne la fonction dérivée de $h$. Pour tout réel $x$ appartenant à l’intervalle $[0;+\infty[$ on a :
- Déterminer une primitive sur l’intervalle $[0; +\infty[$ de la fonction $x\mapsto \text{e}^{-x}$. Une primitive de la fonction $x\mapsto \text{e}^{-x}$ définie sur $[0;+\infty[$ est la fonction définie sur ce même intervalle par $x\mapsto -\text{e}^{-x}$.
- Déduire des deux questions précédentes une primitive de la fonction $h$ sur l’intervalle $[0; +\infty[$ On a $h(x)=\text{e}^{-x}-h'(x)$ pour tout réel $x\geqslant 0$.
$\begin{align*} \text{e}^{-x}-h'(x)&=\text{e}^{-x}-(1-x)\text{e}^{-x} \\
&=\text{e}^{-x}-\text{e}^{-x}+x\text{e}^{-x}\\
&=x\text{e}^{-x}\\
&=h(x)
\end{align*}$
$\quad$
$\quad$
Par conséquent une primitive de la fonction $h$, continue (car dérivable) sur $[0;+\infty[$, est la fonction $H$ définie sur $[0;+\infty[$ par :
$\begin{align*} H(x)&=-\text{e}^{-x}-h(x)\\
&=-\text{e}^{-x}-x\text{e}^{-x}\\
&=-(1+x)\text{e}^{-x}
\end{align*}$
$\quad$
Or $\lim\limits_{x \to +\infty} \dfrac{\text{e}^x}{x}=+\infty$ donc $\lim\limits_{x \to +\infty} h(x)=0^+$.
$\quad$
$f'(x)=\text{e}^{-x}-x\text{e}^{-x} = (1-x)\text{e}^{-x}$
La fonction exponentielle est strictement positive. Par conséquent le signe de $h'(x)$ ne dépend que de celui de $(1-x)$.
$1-x=0\iff x =1$ et $1-x>0\iff x <1$.
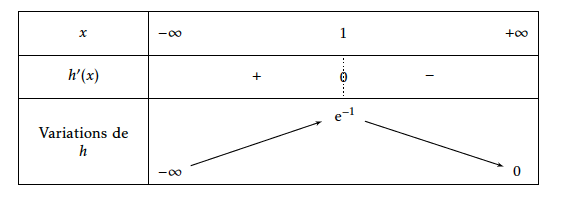
On obtient donc le tableau de variation suivant :
Partie B
On définit les fonctions $f$ et $g$ sur l’intervalle $[0; +\infty[$ par :
$h(x) = x \text{e}^{-x} + \ln(x + 1)$ et $g(x)=\ln(x + 1).$
On note $C_f$ et $C_g$ les représentations graphiques respectives des fonctions $f$ et $g$ dans un repère orthonormé. Ces deux courbes sont tracées en annexe. Cette annexe est à rendre avec la copie.
- Pour un nombre réel $x$ appartenant à l’intervalle $[0; +\infty[$, on appelle $M$ le point de coordonnées $(x; f(x))$ et $N$ le point de coordonnées $(x; g(x))$ : $M$ et $N$ sont donc les points d’abscisse $x$ appartenant respectivement aux courbes $C_f$ et $C_g$.
- Déterminer la valeur de $x$ pour laquelle la distance $MN$ est maximale et donner cette distance maximale. D’après le tableau de variation de la fonction $h$, on a $h(x)=x\text{e}^{-x}\geqslant 0$.
- Placer sur le graphique fourni en annexe les points $M$ et $N$ correspondant à la valeur maximale de $MN$. On obtient le graphique suivant :
Par conséquent, le repère étant orthonormé :
$\begin {align*} MN&=\sqrt{(x-x)^2+\left(f(x)-g(x)\right)^2} \\
&=\sqrt{\left(x\text{e}^{-x}\right)^2} \\
&=x\text{e}^{-x}
\end{align*}$
$\quad$
D’après le tableau de variation de la fonction $h$, cette distance est maximale pour $x=1$ et cette distance maximale vaut $\text{e}^{-1}$
$\quad$
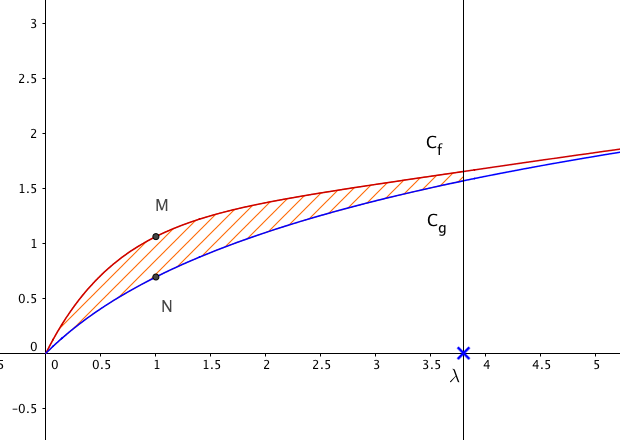
- Soit $\lambda$ un réel appartenant à l’intervalle $[0; +\infty[$. On note $D_{\lambda}$ le domaine du plan délimité par les courbes Cf et Cg et par les droites d’équations $x = 0 $ et $x = \lambda$.
- Hachurer le domaine correspondant à la valeur $\lambda$ proposée sur le graphique en annexe. Voir graphique précédent
- On note $A_{\lambda}$ l’aire du domaine $D_{\lambda}$, exprimée en unités d’aire. Démontrer que : $A_{\lambda}= 1-\dfrac{\lambda +1}{\text{e}^{\lambda}}$ L’aire du domaine $D_{\lambda}$ est :
- Calculer la limite de $A_{\lambda}$ lorsque A tend vers $+\infty$ et interpréter le résultat. On a $A_{\lambda}=1-\dfrac{\lambda}{e^{\lambda}}-\dfrac{1}{\text{e}^{\lambda}}$
$\quad$
On obtient le graphique suivant :
$\begin{align*} A_{\lambda} &=\displaystyle \int_0^{\lambda} \left(f(x)-g(x)\right) dx \\
&=\int_0^{\lambda} x\text{e}^{-x}dx \\
&=H(\lambda)-H(0) \\
&=-(1+\lambda)\text{e}^{-\lambda}+1\\
&=1-\dfrac{\lambda+1}{\text{e}^{\lambda}}
\end{align*}$
$\quad$
Or $\lim\limits_{\lambda \to +\infty} \dfrac{\lambda}{\text{e}^{\lambda}}=0$ (voir la question A.1.)
Et $\lim\limits_{\lambda \to +\infty} \text{e}^{\lambda} = +\infty$ donc $\lim\limits_{\lambda \to +\infty} \dfrac{1}{\text{e}^{\lambda}}=0$
Ainsi $\lim\limits_{\lambda \to +\infty} A_{\lambda}=1$.
$\quad$
Cela signifie que l’aire du domaine compris entre les deux courbe $C_f$ et $C_g$ vaut $1$.
$\quad$ - On considère l’algorithme suivant : $$ \begin{array}{|l |l |}\hline \text{ Variables } & \\ & \lambda \text{ est un réel positif }\\ & S \text{ est un réel strictement positif compris entre 0 et 1. }\\ \text{ Initialisation :}&\\ & \text{ Saisir } S\\ &\lambda \text{ prend la valeur } 0\\ \text{ Traitement :}& \\ &\text{ Tant que }1-\dfrac{\lambda +1}{\text{e}^{\lambda}}< S \text{ faire }\\ &\hspace{0,5cm} \lambda \text{ prend la valeur }\lambda + 1\\ &\text{ Fin Tant que } \\ \text{ Sortie : }& \text{ Afficher } \lambda \\\hline \end{array}$$
- Quelle valeur affiche cet algorithme si on saisit la valeur $S = 0,8$ ? On a $A_0=0$, $A_1\approx 0,2642$, $A_2\approx 0,5940$ et $A_3\approx 0,8009$
- Quel est le rôle de cet algorithme ? L’algorithme renvoie le plus petit entier naturel $\lambda$ pour lequel $A_{\lambda}\geqslant S$.
Donc l’algorithme affichera $3$ si $S=0,8$.
$\quad$
$\quad$
- Vues: 39386